Search: subworld:curves_drawing
|
| |
|
| BP810 |
| Figures can be transformed into one another by smooth stretching (intersection points stay constant; paths connecting those points remain), while remaining within the 2d box vs. movement out of the plane required. |
|
| |
|
| |
| |
|
|
| |
|
| BP854 |
| Nothing vs. nothing. |
|
| |
|
| |
| |
|
|
| |
|
| BP897 |
| Wide angles connected to narrow angles vs. not so. |
|
| |
|
| |
| |
|
|
| |
|
| BP898 |
| Can fold into tetragonal disphenoid ("isosceles tetrahedron") vs. cannot. |
|
| |
|
| |
| |
|
|
| |
|
| BP899 |
| Regions in drawing (ignore background) can be coloured using three or fewer colours such that no adjacent regions are coloured the same colour vs. four colours are required. |
|
| |
|
| |
| |
|
|
| |
|
| BP905 |
| Graph can be redrawn such that no edges intersect vs. not so. |
|
| |
|
| |
| |
|
|
| |
|
| BP924 |
| Polygons where all sides are different lengths vs. Polygons where not all sides are different lengths. |
|
| |
|
|
|
|
COMMENTS
|
All examples in this Problem are outlines of convex polygons.
This is a generalisation of scalene triangles to any polygon. |
|
|
CROSSREFS
|
The left side implies the right side of BP329 (regular vs. irregular polygons), but the converse is not true.
The left side of BP329 implies the right side, but the converse is not true.
Adjacent-numbered pages:
BP919 BP920 BP921 BP922 BP923 * BP925 BP926 BP927 BP928 BP929
|
|
|
EXAMPLE
|
Any scalene triangle will fit on the left, because no two sides are equal.
However, any regular polygon will not fit on the left, because all of its sides are equal.
A random convex polygon will "almost surely" fit on the left. |
|
|
KEYWORD
|
nice, stretch, right-narrow, traditional
|
|
|
CONCEPT
|
all (info | search)
|
|
|
WORLD
|
polygon_outline [smaller | same | bigger]
|
|
|
AUTHOR
|
Jago Collins
|
| |
|
|
| |
|
| BP932 |
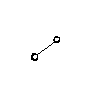
| Every vertex is connected to every other vs. vertices are connected in a cycle (no other connections). |
|
| ?
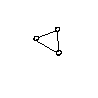 | ?
 |
|
|
|
|
|
COMMENTS
|
Complete graphs with zero, one, two, or three vertices would be ambiguously categorized (fit in overlap of both sides).
Left examples are called "fully connected graphs." Right examples are called "cycle graphs." |
|
|
CROSSREFS
|
Adjacent-numbered pages:
BP927 BP928 BP929 BP930 BP931 * BP933 BP934 BP935 BP936 BP937
|
|
|
KEYWORD
|
precise, left-narrow, right-narrow, both, preciseworld
|
|
|
CONCEPT
|
graph (info | search),
distinguishing_crossing_curves (info | search),
all (info | search),
loop (info | search)
|
|
|
WORLD
|
connected_graph [smaller | same | bigger]
|
|
|
AUTHOR
|
Aaron David Fairbanks
|
| |
|
|
| |
| |
| |
|
|
|
|
REFERENCE
|
Henneberg, L. (1911), Die graphische Statik der starren Systeme, Leipzig
Jackson, Bill. (2007). Notes on the Rigidity of Graphs.
Laman, Gerard. (1970), "On graphs and the rigidity of plane skeletal structures", J. Engineering Mathematics, 4 (4): 331–340.
Pollaczek‐Geiringer, Hilda (1927), "Über die Gliederung ebener Fachwerke", Zeitschrift für Angewandte Mathematik und Mechanik, 7 (1): 58–72. |
|
|
CROSSREFS
|
Adjacent-numbered pages:
BP1011 BP1012 BP1013 BP1014 BP1015 * BP1017 BP1018 BP1019 BP1020 BP1021
|
|
|
KEYWORD
|
nice, physics, help
|
|
|
CONCEPT
|
rigidity (info | search),
graph (info | search),
imagined_motion (info | search)
|
|
|
WORLD
|
planar_connected_graph [smaller | same | bigger]
zoom in left (rigid_planar_connected_graph)
|
|
|
AUTHOR
|
Aaron David Fairbanks
|
| |
|
|
| |
|
| BP1099 |
| Considering only the ways they are connected, anything that can be said about a given node can be said about every other node vs. not so. |
|
| |
|
| |
| |
|
|
Welcome |
Solve |
Browse |
Lookup |
Recent |
Links |
Register |
Contact
Contribute |
Keywords |
Concepts |
Worlds |
Ambiguities |
Transformations |
Invalid Problems |
Style Guide |
Goals |
Glossary
|
|
|
|
|
|
|
|
|
|